Đây là Phần 2 của bài viết gồm hai phần về khả năng xử lý. Phần 1 đề cập đến khái niệm khả năng của quy trình và cách tính toán nó, bao gồm cả những việc cần làm với dữ liệu bình thường và không bình thường. Phần 2 xem xét tỷ lệ hư hỏng và điều kiện vật liệu cho một ví dụ hoàn thiện bề mặt.
Đôi khi, một quy trình có các thông số kỹ thuật là một mặt như độ phẳng, độ vuông góc, độ hoàn thiện bề mặt và độ tròn. Khi đánh giá khả năng của quy trình trong những trường hợp đó, bạn sẽ thực sự xem xét khả năng xử lý cho một nửa phân phối – một nửa không bị cắt bởi đặc điểm kỹ thuật ranh giới. Xây dựng biểu đồ kiểm soát (ImR), biểu đồ xác suất thông thường và sau đó đánh giá khả năng của quá trình. Đây là một ví dụ về nghiên cứu khả năng hoàn thiện bề mặt.
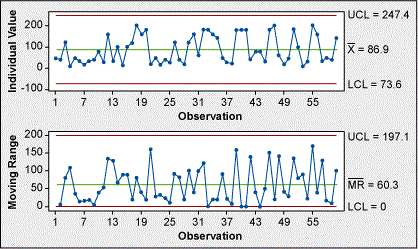
Biểu đồ kiểm soát ổn định và trong tầm kiểm soát (Hình 1).

Hình 1: Ổn định và kiểm soát
Dường như có vấn đề với biểu đồ xác suất thông thường (Hình 2). Dữ liệu không bình thường. Điều tra dữ liệu thêm một chút cho thấy rằng hình dạng có vẻ tiệm cận khi nó tiến gần đến số 0; và phía bên phải của dữ liệu theo một dòng khá tốt. Hàm mật độ xác suất (PDF) của dữ liệu này sẽ giống như một nửa của PDF thông thường.

Hình 2: Đồ thị xác suất thông thường
Trong trường hợp này, không có giá trị nào trong việc ước tính Cpk (thấp hơn) như 0 là giới hạn vật lý và là điều kiện mong muốn nhất. Ví dụ, độ hoàn thiện bề mặt không thể tốt hơn 0. Trong trường hợp này, chỉ báo cáo Cpk (trên). Khi phân tích dữ liệu này, thông số kỹ thuật 0 / thấp hơn được chọn làm ranh giới. Điều này cho phần mềm chỉ ước tính Cpk (thấp hơn).

Hình 3: Ước tính Cpk (trên)
Ước tính tỷ lệ thất bại từ Cpk
Nếu có một quy trình:
- Có mức trung bình là 9,02 ml
- Có độ lệch chuẩn là 0,5 ml
- Có giới hạn thông số kỹ thuật trên (USL) là 12 ml
- Có giới hạn thông số kỹ thuật thấp hơn (LSL) là 8 ml
- Ổn định và trong tầm kiểm soát
- Có dữ liệu tuân theo phân phối chuẩn
thì khả năng xử lý có thể được tính toán.

Hình 4: Tính toán Khả năng của Quy trình
Đánh giá Cpk để thấy rằng con số là .79 như Cpk (thấp hơn) (.79)> Cpk (trên) (2,30). Điểm Z, đôi khi được gọi là mức sigma, có thể được sử dụng để dự đoán tỷ lệ thất bại. Điểm Z có thể được tính toán dễ dàng. Z tương tự như Cpk nơi XTôi là giới hạn đặc điểm kỹ thuật.
![]()
trong đó quan sát cho thấy rằng Z gấp 3 lần Cpk.
Z(phía trên) là 5,95 và Z(thấp hơn) là 2,03. Tra cứu các giá trị này trên một bảng thông thường tiêu chuẩn để biết xác suất vượt quá các giá trị này. Xác suất thất bại ở phía trên là 0 như trong Hình 5 bên dưới. Xác suất thất bại ở phía dưới là 2,095 phần trăm. Chuyển đổi giá trị này thành phần triệu (PPM) và nhận được tỷ lệ lỗi 20.950 PPM.
Cho đến nay, trọng tâm vẫn là khả năng tiềm ẩn hoặc khả năng ngắn hạn. Theo thời gian, trong mỗi trường hợp, một lô vật liệu được lấy mẫu; mẫu tạo ra một phân phối được dịch chuyển từ phân phối mẫu trước đó. Khi tất cả dữ liệu này được gộp chung, phân phối sẽ rộng hơn. Điều này dẫn đến Pp và Ppk. Ppk là khả năng quá trình dài hạn. Nó đôi khi được gọi là hiệu suất quá trình. Nó bao gồm tất cả dữ liệu từ một số mẫu. Sự khác biệt duy nhất trong phép toán giữa ngắn hạn Cpk (trên) và lâu dài Ppk là cách ước tính độ lệch chuẩn. Cpk (trên) sử dụng phương pháp biểu đồ kiểm soát để ước tính độ lệch chuẩn, ![]() như với biểu đồ ImR và Ppk sử dụng tổng bình phương ước tính,
như với biểu đồ ImR và Ppk sử dụng tổng bình phương ước tính,  như với một
như với một ![]() đồ thị.
đồ thị.

Hình 5: Hiệu suất so với giá trị
Cả hai Cpk và Ppk yêu cầu quá trình phải ổn định và được kiểm soát để có hiệu lực. Nếu quá trình ổn định và được kiểm soát, nó sẽ tạo ra sự khác biệt nhỏ về số lượng mà ước tính khả năng được sử dụng. Điều quan trọng nhất là dữ liệu được lấy mẫu sao cho nó bao gồm các biến thể dự kiến và các điều kiện nhiễu. Nhiều tổ chức yêu cầu ngắn hạn Cpksẽ cao hơn dài hạn Ppk‘s – thường bằng hệ số 1,5 độ lệch chuẩn – để đề phòng sự biến đổi bị bỏ lỡ và sự dịch chuyển và trôi dạt bình thường. Người ta thường kỳ vọng giá trị trung bình của các mẫu thay đổi ± 1,5 σ.
Tình trạng vật liệu tối đa hoặc Điều kiện vật liệu thấp nhất Khả năng vị trí thực
Các phép đo khả năng xử lý truyền thống gặp rắc rối khi có điều kiện vật chất tối đa hoặc điều kiện vật chất ít nhất là thông số kỹ thuật vị trí thực.
Hình 6 cho thấy khung điều khiển tính năng Geometric Dimensions & Tolerancing (GD&T). (Tham khảo ASME Y14.5-2009 để biết thêm chi tiết.) Điều này xác định kích thước, vị trí cho lỗ trong ví dụ hoàn thiện bề mặt.

Hình 6: Biểu đồ Kích thước & Tolerancing hình học (GD&T)
Trong tình huống như thế này, đường kính và vị trí không độc lập. Đây là một vấn đề vì tính độc lập là một yêu cầu đối với Cpk, Cp, Ppk và Pp. Điều này đòi hỏi phải sử dụng phân tích đa biến.
Thay vì sử dụng biểu đồ ImR để kiểm tra độ ổn định, hãy sử dụng biểu đồ T2 – biểu đồ phương sai tổng quát. Biểu đồ phương sai tổng quát được coi như biểu đồ phạm vi về đánh giá độ ổn định và T2 biểu đồ được sử dụng để đánh giá kiểm soát. Quá trình này ổn định và được kiểm soát. Trong ví dụ này, dữ liệu được đưa ra dưới dạng đường kính, vị trí thực.

Hình 7: T2– Biểu đồ phương sai tổng quát của đường kính, vị trí thực
| Bảng 1: Dữ liệu Ví dụ | ||
| X nom | Y nom | Dia nom |
| 95,6000 | 113,9000 | 4.6500 |
| Bảng 2: Dữ liệu Ví dụ khác | |||
| Biến đổi | Đếm | Nghĩa là | StDev |
| X | 30 | 95.595 | 0,0144 |
| Y | 30 | 113,88 | 0,0249 |
| Đường kính | 30 | 4,5226 | 0,0341 |
| Vị trí đích thực | 30 | 0,06300 | 0,03168 |
Dữ liệu có dạng tọa độ (X, Y)
Nếu nhà đo lường báo cáo dữ liệu mẫu theo tọa độ X, Y, thì quá trình này rất đơn giản hóa. Thậm chí tốt hơn, Minitab có một macro cho phiên bản 17 để thực hiện phân tích được gọi là POSCAP.MAC.

Hình 8: Các phương trình liên quan
Dẫn đến một máy tínhpk của 7.13.
Để sử dụng Minitab, bạn phải lấy macro POSCAP.MAC. Liên hệ với bộ phận trợ giúp của Minitab để thực hiện việc này. Sau đó, lưu macro này trong thư mục macro của bạn. Khi macro được lưu ở đúng vị trí, hãy đảm bảo bật các lệnh như trong Hình 9.

Hình 9: Cách kích hoạt lệnh
Tổng dung sai đường kính được tính là 0,51.
Để chạy macro, hãy nhập dòng lệnh sau vào dấu nhắc lệnh (MTB>)
MTB>% poscap c1 c2 0,51;
SUBC> Danh nghĩa 95,6 113,9
Danh nghĩa mặc định cho tọa độ X và Y là (0, 0). Một giá trị danh nghĩa khác có thể được nhập cho các tọa độ X, Y như trong trường hợp này (95,6, 113,9). Ngay cả khi chỉ một trong các giá trị danh nghĩa khác không, cả hai giá trị danh nghĩa phải được nhập.
Macro cung cấp hai đầu ra dựa trên hai phân tích. Nó cung cấp một khả năng truyền thống dựa trên vị trí từ danh nghĩa. Đó là khả năng một phía với 0 là ranh giới. Xin lưu ý rằng đây chỉ là phân tích về vị trí. Nó không bao gồm dung sai kích thước hoặc tiền thưởng. Về bản chất, nó thực hiện phép tính được thể hiện trong các phương trình và Hình 10 bên dưới. Nó là một điều kiện biên ở 0 nên nó chỉ báo cáo một Cpk (trên). Macro báo cáo điều này là bù đắp.


Hình 10: Báo cáo khả năng xử lý để bù đắp
Đầu ra thứ hai từ macro là máy tínhpk kết quả cùng với một biểu đồ phân tán X, Y. Nó phủ lên hai vòng tròn: một ở tâm ở danh nghĩa và đại diện cho đường kính dung sai, vòng còn lại ở giữa ở tọa độ trung bình (X, Y) đại diện cho sự thay đổi của quá trình. Tính toán này bao gồm kích thước, vị trí và dung sai thưởng. Nó là một đại diện thực sự của khả năng xử lý cho một chú thích MMC hoặc LMC.

Hình 11: Biểu đồ Tọa độ Vị trí Phân tán
Nếu dữ liệu của bạn ở dạng đường kính, vị trí thực thì việc tính toán trở nên cồng kềnh và không được macro hỗ trợ. Sẽ rất có lợi cho nhà đo lường của bạn khi báo cáo dữ liệu theo tọa độ X, Y. Sau đây là các tính toán cho đường kính, định dạng vị trí thực:
Tài nguyên
- Berardinelli, Carl. “Hướng dẫn Kiểm soát Biểu đồ” iSixSigma.com. Truy cập ngày 30 tháng 3 năm 2017. https://www.isixsigma.com/tools-templates/control-charts/a-guide-to-control-charts/.
- Berardinelli, Carl. “Biểu đồ kiểm soát đa biến: T2 và Phương sai tổng quát,” iSixSigma.com. Truy cập ngày 30 tháng 3 năm 2017. https://www.isixsigma.com/tools-templates/control-charts/multivariate-control-charts-t2-and-generalized-variance/.
- Berardinelli, Carl. “Sử dụng Biểu đồ kiểm soát hoặc Biểu đồ kiểm soát trước” iSixSigma.com. Truy cập ngày 30 tháng 3 năm 2017. https://www.isixsigma.com/tools-templates/control-charts/using-control-charts-or-pre-control-charts/.
- Berardinelli, Carl và Yerian, Lew. “Biểu đồ chạy: Một công cụ đơn giản và mạnh mẽ để cải thiện quy trình,” iSixSigma.com. Truy cập ngày 30 tháng 3 năm 2017. https://www.isixsigma.com/tools-templates/control-charts/run-charts-a-simple-and-powerful-tool-for-process-improvement/.
- Wheeler, Donald J. và Chambers, David S., Hiểu về kiểm soát quy trình thống kê (Tennessee: SPC Press, 1992).
- Hội đồng chất lượng của Indiana. Six Sigma Black Belt Primer được chứng nhận, phiên bản thứ hai (Indiana: Hội đồng Chất lượng của Indiana, 2012).
- Tubiak, TM và Benbow, Donald W. Sổ tay Six Sigma Black Belt được chứng nhận, phiên bản thứ hai (Wisconsin: ASQ Quality Press, 2009).
- Pyzdek, Thomas. Cẩm nang Six Sigma (McGraw-Hill Education, 2003).
- Phần mềm thống kê Minitab V17.
- Krishnamoorthi, KS, “Chỉ số năng lực cho các quy trình tuân theo sự khoan dung về vị trí và đơn phương,” Kỹ thuật chất lượng, Tập 2, Số 4, 461-471.
- Tahan, Antpine và Levesque, Sylvain. (2009). “Khai thác khả năng xử lý dung sai hình học vị trí theo GD&T ASME Y14.5M,” doi: 10.1109 / ICCIE.2009.5223885.
Bạn cũng có thể thích
Nguồn: www.isixsigma.com